The Java platform has long been a cornerstone of enterprise software development, known for its robustness, portability, security, and scalability. As the demand for machine learning (ML) and parallel processing continues to surge across industries, Java is evolving to meet these new computational challenges. This article offers insights into the latest platform enhancements that empower developers to build high-performant, data-driven applications. This in-depth exploration is aimed at experienced Java developers, software architects, and technology enthusiasts who are keen on leveraging Java’s capabilities to innovate in the rapidly growing fields of artificial intelligence and high-performance computing.

Programming and Execution models

Programming and execution models are two fundamental concepts in computing that define how software is designed, developed, and executed. Let’s begin by revisiting some of the key programming and execution models, as that will help us understand the performance benefits that various parallel programming and execution models can offer.

A programming model is an abstraction that defines how a developer writes code to solve a problem. It specifies how data and instructions are structured, how control flows through the program, and how components interact. Some well known programming models include Sequential, Concurrent, and task and data based Parallel programming model.

On the other hand, an execution model defines how a program runs on a computing system, specifying how the instructions are processed by the underlying hardware or software environment. Execution models operate at a lower level, focusing on how the program’s instructions are carried out during runtime. Some examples of execution models include:

• Single Instruction, Single Data (SISD: single processor CPU)
• Multi Instruction, Multi Data (MIMD: multi processor CPU)
• Single Instruction, Multi Data (SIMD: vector or array processors)
• Single Instruction, Multiple Threads (SIMT: GPUs)

SIMD and SIMT models are particularly important for machine learning and other data-intensive tasks. These models enable faster computations by leveraging data-level parallelism, allowing the same operation to be executed simultaneously across multiple data points.

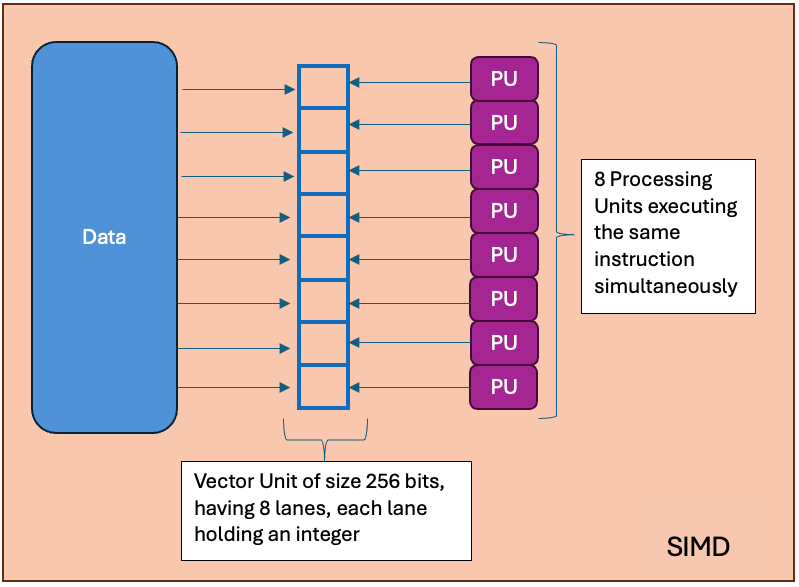
Figure 1: SIMD Block Diagram

In the SIMD model, a single processor performs the same operation simultaneously on different pieces of data, known as vectors. For example, if you need to add two arrays, SIMD can perform several additions in those arrays simultaneously. Most modern CPU architectures offer instruction set extensions for supporting SIMD execution model. For example, Intel X86 processors have instruction set extensions - SSE (Streaming SIMD Extensions) and AVX (Advanced Vector Extensions) - that allow vectorized execution. Modern compilers including the HotSpot Just-In-Time compiler, can automatically optimize (or “vectorize”) loops that iterate over arrays into SIMD instructions.

SIMT offers massive parallelism by concurrent execution of thousands of threads, each performing the same operation but on different data. Graphics Processing Units (GPUs) utilize the SIMT execution model. GPUs have many cores, each with multiple SIMD processors, and SIMT maximizes the utilization of these cores by distributing the workload across a large number of threads, and efficiently context switching between threads which hides any latencies. Threads are grouped into units called warps (NVIDIA) or wavefronts (AMD), which typically consist of 32 or 64 threads. All threads within a warp or wavefront execute the same instruction simultaneously but on different data elements. This results in significantly higher performance, particularly for applications that can exploit data parallelism.

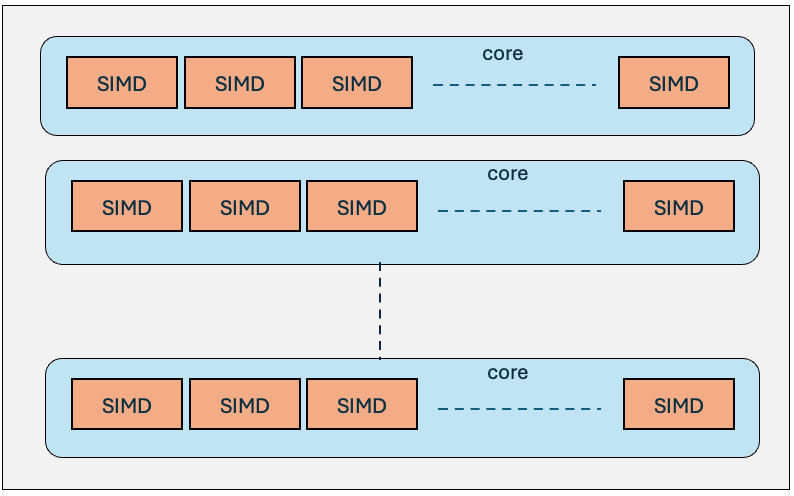
Figure 2: SIMT Block Diagram

Java Platform’s Strides

Let’s examine how the Java Platform has been progressively evolving and continues to evolve to incorporate support for SIMD and SIMT execution models, helping Java developers write code that can effectively harnesses data-parallelism across heterogeneous hardware, including CPUs and GPUs. With these strides, Java is increasingly becoming capable of optimizing performance for data-intensive applications, leveraging the full potential of modern parallel processing architectures.

Panama Vector API

As I mentioned above, the HotSpot JIT compiler can optimize loops that iterate over arrays transforming scalar operations on the array’s elements into equivalent SIMD hardware instructions. While the JIT compiler can automatically vectorize some code, it may not always be able to recognize all opportunities for vectorization, particularly in complex or less obvious scenarios. The Vector API allows developers to explicitly write code that leverages SIMD instructions, ensuring that vectorization is applied where intended.

The Vector API was first proposed by JEP 338 and integrated into JDK 16 as an incubating API. Further rounds of incubation were proposed by JEP 414(integrated into JDK 17), JEP 417(JDK 18), JEP 426(JDK 19), JEP 438(JDK 20), JEP 448(JDK 21), and JEP 460(JDK 22). With JEP 469, this API is available as incubating API in JDK 23.

The Vector API, as described in JEP 469, aims to provide a mechanism for expressing vector computations in Java, allowing developers to write code that can leverage the performance advantages of SIMD hardware capabilities directly. The API provides a set of platform-independent abstractions that map efficiently to the underlying hardware’s vector instructions. This allows developers to write vectorized code in Java that is both portable and optimized for different hardware architectures. Data-intensive tasks, such as those in machine learning, often involve operations on large datasets such as matrix multiplications or element-wise vector operations. The Vector API allows these operations to be executed in parallel across multiple data points, significantly speeding up computations by taking full advantage of SIMD hardware.

The API introduces an abstract class Vector<E> representing a vector, where E corresponds to the boxed type of scalar primitive types like byte, int, float, etc. Each vector has a shape, which defines its size in bits and determines how the vector is mapped to hardware registers during compilation by the HotSpot JIT compiler. The length of a vector or the number of elements is determined by dividing the vector’s size by the element size. The API supports vector shapes of 64, 128, 256, and 512 bits, allowing operations on multiple data elements simultaneously, such as 64 bytes or 16 integers at a time with a 512-bit vector.

Note that the size above refers to the size of hardware vector in bits, and the length indicates the number of elements that can be stored in the vector depending on the element type. In the context of Java’s Vector, its shape refers to the layout of the vector, which encompasses both size and length.

The shape of a vector is defined by VectorSpecies, such as IntVector.SPECIES_128 or FloatVector.SPECIES_256, which determines the element type and the number of elements based on the hardware vector size. Species like SPECIES_PREFERRED allow Java runtime to automatically select the most efficient shape for the platform.

Let’s take a look at an example of adding two arrays using the Vector API.

import jdk.incubator.vector.*;
import java.util.random.RandomGenerator;

public class VectorizedArrayAddition {
    // Define vector shape by dynamically choosing the hardware's optimal vector size
    private static final VectorSpecies<Float> SPECIES = FloatVector.SPECIES_PREFERRED;

    public static void main(String[] args) {
        // SPECIES.length() tells the number of elements that can be stored in a
        // vector. For simplicity, define the size of the arrays as a multiple
        // of SPECIES.length(). This ensures that the entire array can be folded
        // completely into a vector.
        int size = 4 * SPECIES.length();

        // Create two float arrays
        float[] arrayA = new float[size];
        float[] arrayB = new float[size];

        // Populate random values in the input arrays
        RandomGenerator random = RandomGenerator.getDefault();
        for (int i = 0; i < size; i++) {
            arrayA[i] = random.nextFloat();
            arrayB[i] = random.nextFloat();
        }

        // Create an array to store the sum
        float[] result = new float[size];

        // Perform element-wise addition on chunks of arrays using the Vector API.
        // SPECIES.loopBound(size) calculates an upper bound for loop iteration
        // based on the array size, ensuring the loop iterates in multiples
        // of the vector length.
        for (int i = 0; i < SPECIES.loopBound(size); i += SPECIES.length()) {
            // Load chunks of input arrays that can be completely fitted into vectors
            FloatVector va = FloatVector.fromArray(SPECIES, arrayA, i);
            FloatVector vb = FloatVector.fromArray(SPECIES, arrayB, i);

            // Add the two vectors storing the result into a new vector
            FloatVector resultVector = va.add(vb);

            // Store the sum back from the vector into the result array
            resultVector.intoArray(result, i);
        }

        // Print the input and the result arrays
        System.out.println("Array A: ");
        printArray(arrayA);
        System.out.println("Array B: ");
        printArray(arrayB);
        System.out.println("Result (A + B): ");
        printArray(result);
    }

    // Helper method to print an array
    private static void printArray(float[] array) {
        for (float value : array) {
            System.out.printf("%.4f ", value);
        }
        System.out.println();
    }
}

Output from the above program:

Array A:
0.6924 0.6437 0.9361 0.2659 0.6657 0.4424 0.0379 0.3453 0.8392 0.7864 0.0278 0.2217 0.9544 0.6193 0.1928 0.7600 0.6806 0.2778 0.0493 0.6851 0.3882 0.5876 0.9141 0.0223 0.5135 0.6466 0.6999 0.9271 0.9980 0.3014 0.4377 0.4131
Array B:
0.5600 0.2392 0.7359 0.8160 0.3339 0.4383 0.0610 0.7196 0.8142 0.8749 0.0792 0.7448 0.7568 0.3504 0.3881 0.7346 0.5700 0.3781 0.5894 0.2028 0.4706 0.4465 0.4807 0.6917 0.4530 0.2824 0.2955 0.4308 0.1491 0.9397 0.8949 0.9658
Result (A + B):
1.2524 0.8829 1.6720 1.0819 0.9996 0.8807 0.0989 1.0649 1.6534 1.6612 0.1070 0.9666 1.7112 0.9697 0.5809 1.4947 1.2506 0.6559 0.6387 0.8879 0.8588 1.0341 1.3948 0.7140 0.9665 0.9289 0.9954 1.3579 1.1472 1.2411 1.3325 1.3789

VectorSpecies defines the shape of vectors, which is determined by the bit size of the hardware vector and the type of element stored in it. For instance, a VectorSpecies<Float> with a 256-bit size would define a Vector that can store eight float elements (256 bits / 32 bits per float = 8 elements).

Next, the program defines two input arrays arrayA and arrayB and initializes the result array. SPECIES.length() tells the maximum number of elements that can be stored in a vector at the hardware level. The program loads segments of both arrays into FloatVector instances, and then performs addition operation on the vectors, storing the result into resultVector. And finally, the elements from the resultVector are stored into the result array.

This illustrates how the Vector API enables developers to write high-performance, data-parallel Java code that takes full advantage of modern SIMD hardware.

Project Babylon - Code Reflection

In this section, we will talk about the Project Babylon that aims to extend the reach of Java to foreign programming models such as those for GPUs. But first, let’s shift our attention to the SIMT model.

SIMT model and GPUs

SIMT model refers to single instruction executed simultaneously by multiple threads on different data pieces. GPUs(Graphics Processing Units) support this model by leveraging their massively parallel architecture. GPUs are designed to handle thousands of threads concurrently and each thread within a fixed-sized group (often called a warp) executes the same instruction, but on different data. Programming frameworks like CUDA (for NVIDIA GPUs), OpenCL (Open Standard for parallel programming developed by the Khronos Group) and oneAPI (Intel’s cross-architecture unified programming framework) allow developers to write code that explicitly takes advantage of the SIMT model. These frameworks provide abstractions that map directly to the GPU hardware, enabling developers to structure their code to maximize parallel execution. The code written using these frameworks is then compiled into intermediate representations (IRs), later to be converted into the native machine code specific to the GPU architecture. The code gets compiled to an IR called PTX on Nvidia GPUs, SPIR-V on Intel GPUs, and GFX-ISA on AMD GPUs.

Figure 3: GPU Programming Frameworks

In GPU computing, there is a concept of host (CPU) and devices (GPUs). The host initializes the GPU, allocates memory on the GPU, and manages data transfers between the CPU and GPU. The code that can be heavily parallelized is written in a function called a kernel. Kernels are executed on the GPU. The code on the host side, known as compute code, schedules and launches kernels for execution on the GPU, where the execution is handled across its many processing units, and also manages data exchange between the host and devices.

The compute code on host launches a kernel by specifying the number of threads and how they should be organized into blocks and grids. Threads are grouped into blocks, and blocks are grouped into grids. The GPU handles the scheduling and execution of these threads. To understand how threads are grouped and organized, let’s consider CUDA as an example:

• The smallest unit of execution in CUDA is called a warp. It consists of a group of 32 threads that execute the same instruction simultaneously. All threads within a warp execute in lockstep, meaning they all execute the same instruction at the same time.
• A block is a group of threads that execute the same kernel function on the GPU. Each block can contain up to 1024 threads (though the exact maximum can vary depending on the GPU architecture).
• Threads within a block can be indexed using a 1D, 2D, or 3D index, depending on the problem’s dimensionality.
• A grid is a collection of blocks that execute a kernel. Blocks within a grid can also be indexed in 1D, 2D, or 3D. This allows for easy mapping of these blocks to data in multidimensional arrays.

Suppose we have two 2D arrays A and B, each with dimensions 64x64, and we want to add these two arrays element-wise to produce a third array C. There are total 64*64=4096 elements, and 4096 addition operations need to be performed. On a GPU, these operations can be performed simultaneously by launching 4096 threads. Since each block can have up to 1024 threads and each warp 32 threads, two warps can be grouped in a block, allowing 64 threads in each block process a single row of the array. These blocks can be further organized into grids. Two possible configurations for this organization can be:

1. One single grid, having 64 blocks, with two warps per block. The single grid processes 64 rows of the arrays.
2. Two grids, each having 32 blocks, with two warps per block. Each grid processes 32 rows of the arrays.

Here’s a visualization of the second configuration:

Grid 0:
    Block 0:
        Warp 0: Thread 0 -> C[0][0] = A[0][0] + B[0][0]
                Thread 1 -> C[0][1] = A[0][1] + B[0][1]
                ...
                Thread 31 -> C[0][31] = A[0][31] + B[0][31]

        Warp 1: Thread 0 -> C[0][32] = A[0][32] + B[0][32]
                Thread 1 -> C[0][33] = A[0][33] + B[0][33]
                ...
                Thread 31 -> C[0][63] = A[0][63] + B[0][63]

    Block 1:
        Warp 0: Thread 0 -> C[1][0] = A[1][0] + B[1][0]
                Thread 1 -> C[1][1] = A[1][1] + B[1][1]
                ...
                Thread 31 -> C[1][31] = A[1][31] + B[1][31]

        Warp 1: Thread 0 -> C[1][32] = A[1][32] + B[1][32]
                Thread 1 -> C[1][33] = A[1][33] + B[1][33]
                ...
                Thread 31 -> C[1][63] = A[1][63] + B[1][63]
    ...
    Block 31: ...

Grid 1:
    Block 1:
        Warp 0: Thread 0 -> C[32][0] = A[32][0] + B[32][0]
                Thread 1 -> C[32][1] = A[32][1] + B[32][1]
                ...
                Thread 31 -> C[32][31] = A[32][31] + B[32][31]

        Warp 1: Thread 0 -> C[32][32] = A[32][32] + B[32][32]
                Thread 1 -> C[32][33] = A[32][33] + B[32][33]
                ...
                Thread 31 -> C[32][63] = A[32][63] + B[32][63]

    Block 1:
        Warp 0: Thread 0 -> C[33][0] = A[33][0] + B[33][0]
                Thread 1 -> C[33][1] = A[33][1] + B[33][1]
                ...
                Thread 31 -> C[33][31] = A[33][31] + B[33][31]

        Warp 1: Thread 0 -> C[33][32] = A[33][32] + B[33][32]
                Thread 1 -> C[33][33] = A[33][33] + B[33][33]
                ...
                Thread 31 -> C[33][63] = A[33][63] + B[33][63]
    ...
    Block 31: ...

Mapping Java Code to CUDA C

Let’s look at the following Java code performing addition of two large integer arrays.

public class LargeArrayAddition {
    public static void main(String[] args) {
        // Two large integer arrays - array1 and array2
        int[] array1 = new int[1000000];
        int[] array2 = new int[1000000];

        // Initialize arrays with values
        for (int i = 0; i < array1.length; i++) {
            array1[i] = i;
            array2[i] = i * 2;
        }

        // Output array to store the result
        int[] result = new int[array1.length];

        // Add corresponding elements of array1 and array2
        for (int i = 0; i < array1.length; i++) {
            result[i] = array1[i] + array2[i];
        }

        // Print the result
        System.out.println("Sum of the first elements: " + result[0]);
        System.out.println("Sum of the last elements: " + result[result.length - 1]);
    }
}

The loop performing addition of arrays can be heavily parallelized on a GPU, performing all the million addition operations simultaneously. To carry out this addition on a GPU using the CUDA programming model (which applies similarly to other GPU runtimes), we need to follow these steps:

1. Write a kernel function performing the addition operation that can be executed on device (GPU).
2. Allocate arrays on host (CPU).
3. Allocate memory on device (GPU).
4. Copy arrays from host to device.
5. Launch the kernel to add arrays on the GPU.
6. Copy the result array from device to host.
7. Free device memory.
8. Free arrays allocated on host.

Below is the CUDA C code equivalent to the previous Java snippet.

#include <cuda_runtime.h>
#include <iostream>

// define kernel function that adds two large arrays
__global__ void addArrays(int *a, int *b, int *result, int n) {
    int i = blockIdx.x * blockDim.x + threadIdx.x;
    if (i < n) {
        result[i] = a[i] + b[i];
    }
}

int main() {
    const int N = 1000000;
    int *a, *b, *result;
    int *d_a, *d_b, *d_result;

    // Allocate host memory
    a = new int[N];
    b = new int[N];
    result = new int[N];

    // Initialize arrays on the host
    for (int i = 0; i < N; ++i) {
        a[i] = i;
        b[i] = i * 2;
    }

    // Allocate device memory
    cudaMalloc((void**)&d_a, N * sizeof(int));
    cudaMalloc((void**)&d_b, N * sizeof(int));
    cudaMalloc((void**)&d_result, N * sizeof(int));

    // Copy arrays from host to device
    cudaMemcpy(d_a, a, N * sizeof(int), cudaMemcpyHostToDevice);
    cudaMemcpy(d_b, b, N * sizeof(int), cudaMemcpyHostToDevice);

    // Launch the kernel to add arrays on the GPU
    int threadsPerBlock = 256;
    int blocksPerGrid = (N + threadsPerBlock - 1) / threadsPerBlock;
    addArrays<<<blocksPerGrid, threadsPerBlock>>>(d_a, d_b, d_result, N);

    // Copy the result array from device to host
    cudaMemcpy(result, d_result, N * sizeof(int), cudaMemcpyDeviceToHost);

    // Output the result
    std::cout << "Sum of the first elements: " << result[0] << std::endl;
    std::cout << "Sum of the last elements: " << result[N - 1] << std::endl;

    // Free device memory
    cudaFree(d_a);
    cudaFree(d_b);
    cudaFree(d_result);

    // Free host memory
    delete[] a;
    delete[] b;
    delete[] result;

    return 0;
}

Please refer to the CUDA runtime documentation if you are interested in digging deeper into the above CUDA C code.

An important thing to note here is that the speed achieved with parallelism in this simple example may not offset the cost of data exchange between the host and devices.

While launching the kernel, the compute code above is also specifying the organization of threads, blocks and grid, i.e. the number of threads per block and the number of blocks per grid for executing the kernel on the device.

As is obvious from the above example, we need a kernel function and compute code for GPU computing. Can we do this in Java code? What if we could express our intent in Java code to designate a specific part of the code as a kernel function to be executed on a GPU, while also set up compute code to handle data exchange and launch of the kernel?

This will be made possible with Project Babylon and code reflection.

Java Code Models

Project Babylon’s primary goal is to extend the reach of Java to foreign programming models such as those for GPUs. Babylon will achieve this with an enhancement to reflective programming in Java, called code reflection. Code reflection gives access to the code of a method body as a code model, a symbolic representation of the method’s code. Code models are designed to facilitate the analysis and transformation of Java code into forms suitable for execution on different platforms, including GPUs. The code models are intermediate representations of Java code that retain type and structural information, which are essential for transforming Java code into foreign programming models.

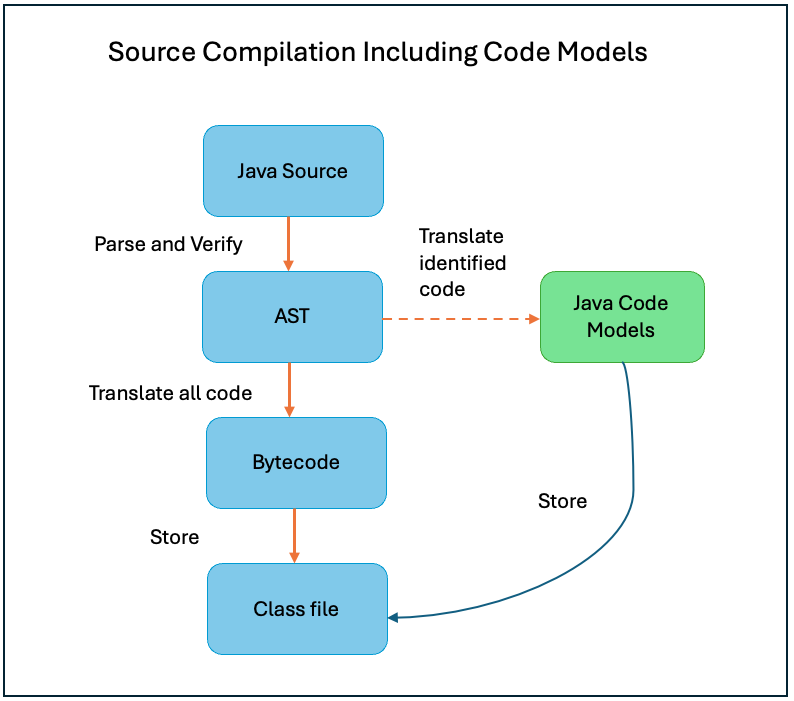
Figure 4: Java Code Models

Transforming Java Code Model to GPU Kernels

A code model in Java, as proposed by Project Babylon, gives access to Java code of identified methods and lambda bodies at compile and runtime. Methods and lambda bodies can be denoted (code performing data-intensive processing and can be parallelized) for identification. The code models of the identified code can later be transformed to kernel functions for execution on GPU.

A Java code model contains operations, bodies, and blocks, organized in a tree structure. Blocks within a body are interconnected with each other to form a control graph. Blocks connect to other block passing values as block parameters. Values are interconnected with each other too and form expression or use graphs. Analysis of these graphs can help Java programs/libraries understand the control and data flow enabling them to construct compute code for launching kernels and performing efficient data exchange between Java and GPU runtimes. This project will also make APIs available to access and manipulate various elements of code models.

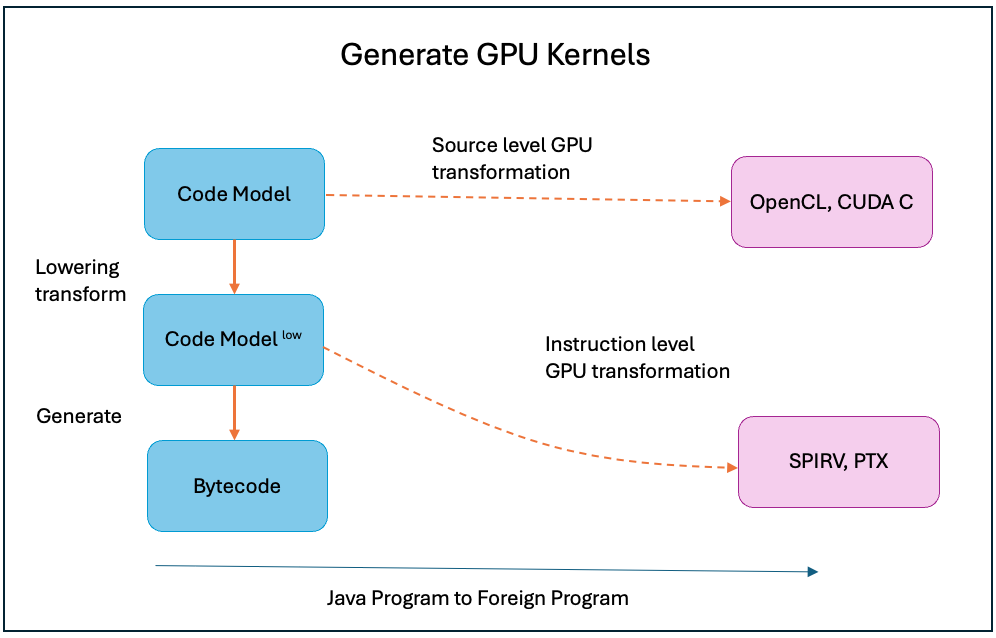
Figure 5: Transformation from code models at different levels to high level representations and IRs for various GPU programming models.

Project Babylon proposes to use annotations (example: @CodeReflection) to identify methods for transformation into code models. For example, in the following code, the add method is annotated so that its code model gets generated and is available for analysis and transformation at compile and runtime.

// Identify a method by annotating it
@CodeReflection
static double add(double a, double b) {
    return a + b;
}

// Access the code model using reflection
// Reflect on "add" method
Method addMethod = MethodExample.class.getDeclaredMethod("add", double.class, double.class);

// Get "add" method's code model
Optional<? extends Op> optionalModel = addMethod.getCodeModel();
Op addCodeModel = optionalModel.orElseThrow();

Leveraging these code models, a Java program or library can perform the following steps to analyze and transform them to foreign programming models.

• The Java compiler (javac) generates a code model from the Java source code. This involves converting the abstract syntax tree (AST) of the Java program into a code model that retains the necessary structural and type information. The following shows how the proposed code model extracted from the class file for the above example method add may look like.

System.out.println(addCodeModel.toText());

func @"add" @loc="11:5:file:/.../MethodExample.java" (%0 : double, %1 : double) double -> {
    %2 = Var<double> = var %0 @"a" @loc="11:5";
    %3 = Var<double> = var %1 @"b" @loc="11:5";
    %4 : double = var.load %2 @loc="13:16";
    %5 : double = var.load %3 @loc="13:20";
    %6 : double = add %4 %5 @loc="13:16";
    return %6 @loc="13:9";
};

• Analyze the code model to identify portions of the code that can be parallelized and executed as kernels on GPU. This will also involve understanding the control flow and data dependencies within the code model to generate compute code responsible for managing optimized data exchange and launching kernels.

• Transform the analyzed code model into GPU kernel code. For example, for OpenCL, this would involve generating C-like kernel code that can be compiled and executed on an OpenCL-compatible device, and for CUDA, the transformation would generate CUDA C/C++ code that can be executed on NVIDIA GPUs.

• Generate compute code from the analyzed model and integrate it back into the Java application. The compute code will perform the necessary data transfers between the Java application and the GPU, launching the kernel, and retrieving the results.

This outlines how a Java library can leverage Code Reflection and transform Java code models into the code that can run on GPUs, thereby supporting necessary efficiency for complex calculations required by AI and Machine Learning algorithms. The biggest challenge, however, is managing and coordinating data transfer between the CPU and GPU. Where should the data be allocated ensuring it can be accessed safely by the JVM and the GPU runtimes? If it is allocated on the Java Heap, there is a risk of data getting moved behind-the-scenes by the Garbage Collection (GC) process. While it’s possible to pin memory and lock garbage collection out using Java Native Interface (JNI) functions such as GetPrimitiveArrayCritical, this approach comes with its own set of limitations and potential performance drawbacks.

Fortunately, the Panama FFM API offers an effective solution by providing an easier and performant way for accessing and managing off-heap memory.

Panama FFM API

The Panama Foreign Function & Memory (FFM) API is a feature made final since Java 22 to simplify and enhance the interaction between Java applications and native code or memory outside the Java runtime. This API allows Java programs to efficiently call native functions and access native memory, removing the complexities and safety risks associated with the traditional Java Native Interface (JNI). The FFM API resides in the java.lang.foreign package of the java.base module.

Let’s take a look at some of the key components of this API.

• MemorySegment provides an abstraction over a contiguous region of memory, located either on-heap or off-heap. All memory segments provide spatial and temporal bounds which ensure that memory access operations are safe.

// Allocates 100 bytes of native memory segment
MemorySegment segment = MemorySegment.allocateNative(100);

• Arena models the lifecycle of one or more memory segments. All segments allocated in an arena share the same lifetime. When memory is allocated within an arena, all segments are tied to that arena’s lifecycle, meaning they are automatically deallocated when the arena is closed. This makes memory management easier and reduces the risk of memory leaks. The lifetime of a segment is determined by the type of Arena it is allocated in, which can be global, automatic, confined or shared.

// Allocate a memory segment of 100 bytes in global arena, where it stays always accessible
MemorySegment data = Arena.global().allocate(100);

• MemoryLayout describes the structure of memory segments, including sizes, alignments, and nested data layouts. This helps in modeling complex data structures.

// Layout for a 4-byte integer
MemoryLayout intLayout = ValueLayout.JAVA_INT;

// Layout for a struct with an int and a float
MemoryLayout structLayout = MemoryLayout.structLayout(
    ValueLayout.JAVA_INT.withName("x"),
    ValueLayout.JAVA_FLOAT.withName("y")
);

• ValueLayout is a specialized form of MemoryLayout that describes the memory layout of primitive data types such as integers, floats, or other scalar values. It allows us to precisely define how these values are stored in memory, including details like byte order (endianness) and size.

// ValueLayout for an integer
ValueLayout intLayout = ValueLayout.JAVA_INT;

Given previous examples, this API facilitates native memory allocations that can map to native data types and structures. These memory segments can be passed as parameters to kernel functions that can be safely exchanged between the Java and non-Java runtimes (CUDA runtime). Consider the following example that performs the addition of two large arrays allocated outside of Java Heap using the FFM API. This example maps to the one we had examined above performing addition of two primitive arrays allocated in the Java Heap.

import java.lang.foreign.Arena;
import java.lang.foreign.MemorySegment;
import java.lang.foreign.ValueLayout;

public class FFMArrayAddition {
    public static void main(String[] args) {
        int arraySize = 1000000;
        try (Arena arena = Arena.ofConfined()) {
            // Allocate memory for the arrays
            MemorySegment array1 = arena.allocate(arraySize * ValueLayout.JAVA_INT.byteSize());
            MemorySegment array2 = arena.allocate(arraySize * ValueLayout.JAVA_INT.byteSize());
            MemorySegment result = arena.allocate(arraySize * ValueLayout.JAVA_INT.byteSize());

            // Initialize arrays
            for (int i = 0; i < arraySize; i++) {
                array1.setAtIndex(ValueLayout.JAVA_INT, i, i);
                array2.setAtIndex(ValueLayout.JAVA_INT, i, i * 2);
            }

            // Perform addition, which could be converted to a kernel function to be
            // executed on a GPU.
            for (int i = 0; i < arraySize; i++) {
                int sum = array1.getAtIndex(ValueLayout.JAVA_INT, i) +
                          array2.getAtIndex(ValueLayout.JAVA_INT, i);
                result.setAtIndex(ValueLayout.JAVA_INT, i, sum);
            }
        }
    }
}

Here, the large integer arrays are allocated outside of the Java Heap. Notice that the loop containing the addition operation could be converted to a kernel function and this intent can be expressed here for this loop, and leveraging Code Reflection the loop can then be transformed to a kernel function understandable by GPU runtimes.

Similarly, we can allocate complex structures in native memory using this API. Consider the following C struct holding integer x and y variables:

struct Point {
    int x;
    int y;
} pt;

We can define a MemoryLayout to the same effect with the FFM API.

MemoryLayout structLayout = MemoryLayout.structLayout(
            ValueLayout.JAVA_INT.withName("x"),
            ValueLayout.JAVA_INT.withName("y")
).withName(pt);

// Allocate memory for the structure
MemorySegment structSegment = arena.allocate(structLayout);

Look how elegantly the FFM API has resolved allocating off-heap data for exchange between the host and devices, marking a huge stride in AI advancement using Java! Now, how do we express the intent of converting a certain piece of code into a kernel and for setting up the compute code for launching it? That brings us to an ongoing effort of building a toolkit named ** Heterogenous Accelerator Toolkit (HAT)** that leverages Code Reflection to do exactly that.

Heterogenous Accelerator Toolkit (HAT)

HAT aims to enable Java programs to leverage GPU acceleration, building on top of Code Reflection and FFM API. Its goal is to provide a programming model closer to traditional GPU programming (like CUDA or OpenCL) rather than trying to hide it behind Java-specific APIs.

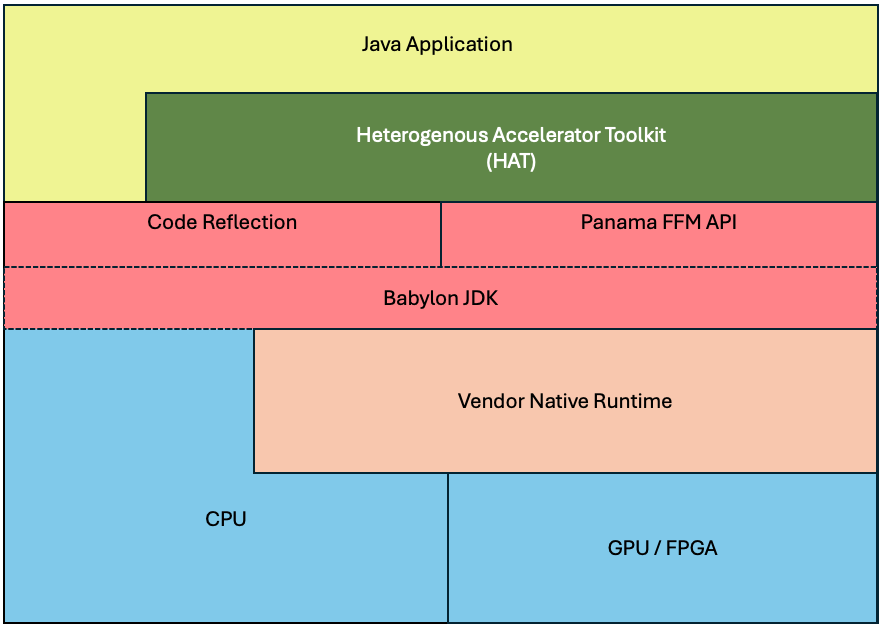
Figure 6: HAT Block Diagram

This toolkit will target heterogenous accelerated processors (CPUs, GPUs, FPGAs, etc.) and proposes to offer the following as part of its API:

• KernelContext

  HAT proposes KernelContext that abstracts vendor-specific mechanisms for identifying kernels or work-items and managing those work-items within a computational grid or range. ​ It is similar to NDRange (N-Dimensional Range) API in GPU programming models. NDRange is a concept in parallel computing, particularly in OpenCL, that represents the organization of work-items (parallel execution units) in a multi-dimensional space. An NDRange example is organization of work-items (e.g. addition or multiplication operation) into threads, blocks and grids.

  KernelContext will provide fields like kc.x, kc.maxX, kc.group.x and kc.group.maxX to identify each kernel, handle data responsibilities, and coordinate parallel processing efficiently. It supports 1D (one-dimensional) ranges initially and may extend to 2D and 3D ranges (KernelContext2D and KernelContext3D) in the future. ​ It also offers a vendor-neutral namespace for accessing GPU runtime APIs and enables mapping of kernel identity and execution specifics within the HAT framework.

• ComputeContext

  ComputeContext represents the compute method, and contains a call-graph constructed from Java code models of the compute method and all the methods that are transitively invoked from it. For each kernel dispatched from this compute call-graph, the ComputeContext maps a kernel call-graph to the appropriate dispatchKernel method in the graph.

• Common wraps for FFM MemoryLayout

  The FFM API simplifies coordinating memory between JVM and GPU runtimes. HAT proposes to offer wrapped data types over FFM MemoryLayouts, types representing Matrices, 1D, 2D and 3D arrays, Images and so on. These wrappers will make it easy to map data layouts on the Java side to what GPU runtimes understand and expect. For example, S32Arr represents a one dimensional array holding 32-bit sized elements.

• Accelerator

  Accelerator provides an abstraction over vendor specific GPU runtime such as CUDA, OpenCL or OneAPI. The interface implementations will be responsible for converting the Java code model into code compatible with specific GPU runtimes, as well as managing the mapping and transfer of data between Java and these GPU environments.

Let’s take a look at the following example that utilizes the proposed HAT API:

    @CodeReflection
    public static int squareit(int v) {
        return  v * v;

    }
    @CodeReflection
    public static void squareKernel(KernelContext kc, S32Array s32Array) {
        if (kc.x<kc.maxX){
           int value = s32Array.array(kc.x);       // arr[cc.x]
           s32Array.array(kc.x, squareit(value));  // arr[cc.x]=value*value
        }
    }
    @CodeReflection
    public static void square(ComputeContext cc, S32Array s32Array) {
        cc.dispatchKernel(s32Array.length(),
                kc -> squareKernel(kc, s32Array)
        );
    }
    public static void main(String[] args) {
        var lookup = java.lang.invoke.MethodHandles.lookup();
        var accelerator = new Accelerator(lookup, Backend.FIRST);
        var arr = S32Array.create(accelerator, 32);
        for (int i = 0; i < arr.length(); i++) {
            arr.array(i, i);
        }
        accelerator.compute(cc -> Main.square(cc, arr)
        );

        System.out.println("##### Printing array #####");
        for (int i = 0; i < arr.length(); i++) {
            System.out.println(i + " " + arr.array(i));
        }
    }

The CodeReflection annotation at the top of squareit() , square(), and squareKernel() methods indicates that the Java code models for these methods will get generated. square() and squareKernel() methods represent the compute and kernel functions respectively.

What exactly are the HAT API calls doing in this program? For executing a compute method, we first create an Accelerator, which is bound to a vendor provided Backend. An accelerator backend for a specific GPU runtime transforms the kernel code into the code for that runtime. Next, we create an array associating it with the accelerator instance. The accelerator.compute() creates a ComputeContext and invokes the compute method. The ComputeContext in the compute method dispatches a kernel by creating a KernelContext identifying a kernel or work-item. The kernel method performs the square operation on an element of the input array, and kc.x provides the index of that element in a specific kernel.

Let’s look at the various transformations that the above program undergoes using the HAT toolkit. First, the Code Reflection produces the following code models for the annotated methods:

func @"square" @loc="50:5:file:///home/poonam/poonam/squares/Main.java" (%0 : hat.ComputeContext, %1 : hat.buffer.S32Array)void -> {
    %2 : Var<hat.ComputeContext> = var %0 @"cc" @loc="50:5";
    %3 : Var<hat.buffer.S32Array> = var %1 @"s32Array" @loc="50:5";
    %4 : hat.ComputeContext = var.load %2 @loc="52:9";
    %5 : hat.buffer.S32Array = var.load %3 @loc="52:27";
    invoke %0 %5 @"hat.ComputeContext::preAccess(hat.buffer.Buffer)void";
    %6 : int = invoke %5 @"hat.buffer.S32Array::length()int" @loc="52:27";
    invoke %0 %5 @"hat.ComputeContext::postAccess(hat.buffer.Buffer)void";
    %7 : hat.ComputeContext$QuotableKernelContextConsumer = lambda @loc="53:17" (%8 : hat.KernelContext)void -> {
        %9 : Var<hat.KernelContext> = var %8 @"kc" @loc="53:17";
        %10 : hat.KernelContext = var.load %9 @loc="53:36";
        %11 : hat.buffer.S32Array = var.load %3 @loc="53:40";
        invoke %10 %11 @"squares.Main::squareKernel(hat.KernelContext, hat.buffer.S32Array)void" @loc="53:23";
        return @loc="53:17";
    };
    invoke %4 %6 %7 @"hat.ComputeContext::dispatchKernel(int, hat.ComputeContext$QuotableKernelContextConsumer)void" @loc="52:9";
    return @loc="50:5";
};

func @"squareKernel" @loc="42:5:file:///home/poonam/poonam/squares/Main.java" (%0 : hat.KernelContext, %1 : hat.buffer.S32Array)void -> {
    %2 : Var<hat.KernelContext> = var %0 @"kc" @loc="42:5";
    %3 : Var<hat.buffer.S32Array> = var %1 @"s32Array" @loc="42:5";
    %4 : hat.KernelContext = var.load %2 @loc="44:13";
    %5 : int = field.load %4 @"hat.KernelContext::x()int" @loc="44:13";
    %6 : hat.KernelContext = var.load %2 @loc="44:18";
    %7 : int = field.load %6 @"hat.KernelContext::maxX()int" @loc="44:18";
    %8 : boolean = lt %5 %7 @loc="44:13";
    cbranch %8 ^block_1 ^block_2;

  ^block_1:
    %9 : hat.buffer.S32Array = var.load %3 @loc="45:24";
    %10 : hat.KernelContext = var.load %2 @loc="45:39";
    %11 : int = field.load %10 @"hat.KernelContext::x()int" @loc="45:39";
    %12 : long = conv %11 @loc="45:24";
    %13 : int = invoke %9 %12 @"hat.buffer.S32Array::array(long)int" @loc="45:24";
    %14 : Var<int> = var %13 @"value" @loc="45:12";
    %15 : hat.buffer.S32Array = var.load %3 @loc="46:12";
    %16 : hat.KernelContext = var.load %2 @loc="46:27";
    %17 : int = field.load %16 @"hat.KernelContext::x()int" @loc="46:27";
    %18 : long = conv %17 @loc="46:12";
    %19 : int = var.load %14 @loc="46:42";
    %20 : int = invoke %19 @"squares.Main::squareit(int)int" @loc="46:33";
    invoke %15 %18 %20 @"hat.buffer.S32Array::array(long, int)void" @loc="46:12";
    branch ^block_3;

  ^block_2:
    branch ^block_3;

  ^block_3:
    return @loc="42:5";
};

Next, the HAT toolkit transforms the above code models into the following CUDA C code.

#define NDRANGE_CUDA
#define __global
typedef char s8_t;
typedef char byte;
typedef char boolean;
typedef unsigned char u8_t;
typedef short s16_t;
typedef unsigned short u16_t;
typedef unsigned int u32_t;
typedef int s32_t;
typedef float f32_t;
typedef long s64_t;
typedef unsigned long u64_t;
typedef struct KernelContext_s{
    int x;
    int maxX;
}KernelContext_t;
typedef struct S32Array_s{
    int length;
    int array[1];
}S32Array_t;

extern "C" __device__ inline int squareit(
    int v
){
    return v*v;
}
extern "C" __global__ void squareKernel(
     KernelContext_t *kc,  S32Array_t* s32Array
){
    kc->x=blockIdx.x*blockDim.x+threadIdx.x;
    if(kc->x<kc->maxX){
        int value = s32Array->array[(long)kc->x];
        s32Array->array[(long)kc->x]=squareit(value);
    }
    return;
}

And then, the above CUDA C code gets compiled into the PTX code that is executed on the GPU.

.version 7.5
.target sm_52
.address_size 64

	// .globl	squareKernel

.visible .entry squareKernel(
	.param .u64 squareKernel_param_0,
	.param .u64 squareKernel_param_1
)
{
	.reg .pred 	%p<2>;
	.reg .b32 	%r<8>;
	.reg .b64 	%rd<7>;

	ld.param.u64 	%rd2, [squareKernel_param_0];
	ld.param.u64 	%rd1, [squareKernel_param_1];
	cvta.to.global.u64 	%rd3, %rd2;
	mov.u32 	%r2, %ntid.x;
	mov.u32 	%r3, %ctaid.x;
	mov.u32 	%r4, %tid.x;
	mad.lo.s32 	%r1, %r3, %r2, %r4;
	st.global.u32 	[%rd3], %r1;
	ld.global.u32 	%r5, [%rd3+4];
	setp.ge.s32 	%p1, %r1, %r5;
	@%p1 bra 	$L__BB0_2;

	cvta.to.global.u64 	%rd4, %rd1;
	mul.wide.s32 	%rd5, %r1, 4;
	add.s64 	%rd6, %rd4, %rd5;
	ld.global.u32 	%r6, [%rd6+4];
	mul.lo.s32 	%r7, %r6, %r6;
	st.global.u32 	[%rd6+4], %r7;

$L__BB0_2:
	ret;
}

That’s amazing! Leveraging code models, the HAT library transforms Java code, enabling it to run seamlessly on GPUs or other accelerated devices.

Note that Code Reflection and HAT are not currently included in the JDK; they are part of the Project Babylon repository. Future versions of the JDK may incorporate features from Project Babylon, and the features mentioned here may also evolve.

Other Related Work

In this section, I want to highlight a few other initiatives aimed at enabling the execution of Java code on heterogeneous hardware, including GPUs.

TornadoVM is a plug-in to OpenJDK and GraalVM, and represents a framework that allows Java code to run on heterogeneous hardware, such as GPUs, FPGAs, and multi-core CPUs, without requiring code rewrites in specialized languages like CUDA or OpenCL. It introduces an API that allows Java developers to mark Java code sections that can be executed in parallel using annotations like @Parallel. It also provides an API to build a pipeline of multiple tasks, and the dependencies and optimizations between those tasks are automatically managed by its runtime. TornadoVM integrates with the GraalVM JIT compiler, which is augmented to transform Java bytecode into OpenCL, CUDA, or other low-level instructions suitable for various hardware accelerators. TornadoVM currently supports three backends that generate OpenCL C, NVIDIA CUDA PTX assembly, and SPIR-V binary. Please see more details on this project here.

Aparapi (A Parallel API) is also a Java framework designed to execute Java code on a GPU for parallel processing by leveraging OpenCL. Aparapi uses JNI (Java Native Interface) to interface with native OpenCL libraries, enabling the execution of Java kernels on GPU hardware. In Aparapi, a Kernel class is defined which contains a run() method that operates on data in parallel. Using JNI, Kernel translates the data-parallel code into OpenCL code. JNI also manages the data transfer between the JVM and the GPU, executes OpenCL code, and retrieves results from devices. In case a GPU is unavailable, Aparapi falls back to CPU execution. You can read more on this project here.

Summary

To summarize, in this article, we explored how advancements in the Java platform are enhancing its ability to run on heterogeneous hardware and parallel architectures. Java’s new capabilities, like the Vector API, allow developers to write code that takes advantage of SIMD instructions, improving performance on modern CPUs. The Panama Foreign Function and Memory (FFM) API facilitates interaction with native libraries and memory, removing the complexities associated with the Java Native Interface (JNI). Furthermore, Project Babylon and HAT (Heterogeneous Accelerator Toolkit) aim to enable running of Java code on GPUs, FPGAs, and other accelerators. Together, these enhancements position Java as a robust platform for harnessing data-parallelism on diverse hardware platforms, including CPUs and GPUs, which will significantly accelerate advancements in AI by enabling efficient computations across heterogeneous systems.